Uncertainty Visualization of Critical Points of 2D Scalar Fields for Parametric and Nonparametric Probabilistic Models
Tushar M. Athawale - Oak Ridge National Laboratory, Oak Ridge, United States
Zhe Wang - Oak Ridge National Laboratory, Oak Ridge, United States
David Pugmire - Oak Ridge National Laboratory, Oak Ridge, United States
Kenneth Moreland - Oak Ridge National Laboratory, Oak Ridge, United States
Qian Gong - Oak Ridge National Laboratory, Oak Ridge, United States
Scott Klasky - Oak Ridge National Laboratory, Oak Ridge, United States
Chris R. Johnson - University of Utah, Salt Lake City, United States
Paul Rosen - University of Utah, Salt Lake City, United States
Download preprint PDF
Room: Bayshore VI
2024-10-18T13:06:00ZGMT-0600Change your timezone on the schedule page
2024-10-18T13:06:00Z
Fast forward
Full Video
Keywords
Topology, uncertainty, critical points, probabilistic analysis
Abstract
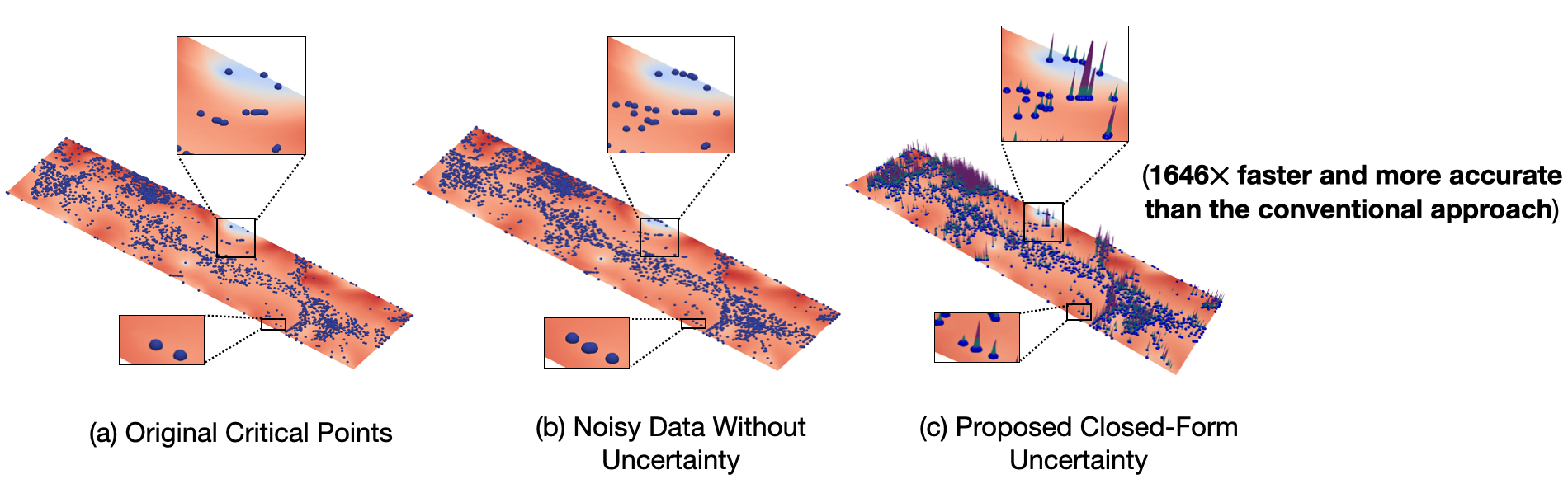
This paper presents a novel end-to-end framework for closed-form computation and visualization of critical point uncertainty in 2D uncertain scalar fields. Critical points are fundamental topological descriptors used in the visualization and analysis of scalar fields. The uncertainty inherent in data (e.g., observational and experimental data, approximations in simulations, and compression), however, creates uncertainty regarding critical point positions. Uncertainty in critical point positions, therefore, cannot be ignored, given their impact on downstream data analysis tasks. In this work, we study uncertainty in critical points as a function of uncertainty in data modeled with probability distributions. Although Monte Carlo (MC) sampling techniques have been used in prior studies to quantify critical point uncertainty, they are often expensive and are infrequently used in production-quality visualization software. We, therefore, propose a new end-to-end framework to address these challenges that comprises a threefold contribution. First, we derive the critical point uncertainty in closed form, which is more accurate and efficient than the conventional MC sampling methods. Specifically, we provide the closed-form and semianalytical (a mix of closed-form and MC methods) solutions for parametric (e.g., uniform, Epanechnikov) and nonparametric models (e.g., histograms) with finite support. Second, we accelerate critical point probability computations using a parallel implementation with the VTK-m library, which is platform portable. Finally, we demonstrate the integration of our implementation with the ParaView software system to demonstrate near-real-time results for real datasets.