Inclusion Depth for Contour Ensembles

Fast forward

Full Video

Keywords

Uncertainty visualization, contours, ensemble summarization, depth statistics.

Abstract

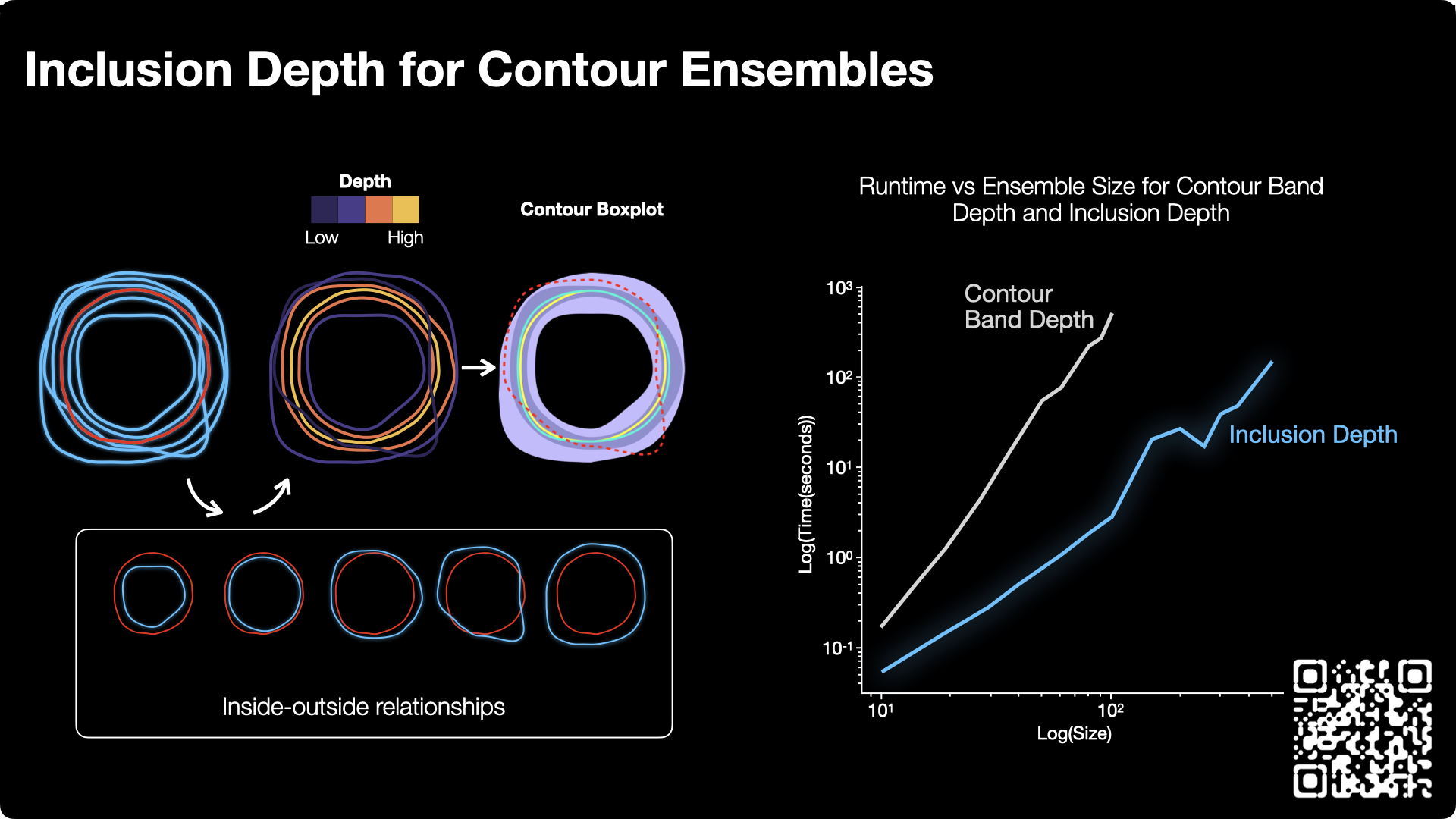
Ensembles of contours arise in various applications like simulation, computer-aided design, and semantic segmentation. Uncovering ensemble patterns and analyzing individual members is a challenging task that suffers from clutter. Ensemble statistical summarization can alleviate this issue by permitting analyzing ensembles' distributional components like the mean and median, confidence intervals, and outliers. Contour boxplots, powered by Contour Band Depth (CBD), are a popular non-parametric ensemble summarization method that benefits from CBD's generality, robustness, and theoretical properties. In this work, we introduce Inclusion Depth (ID), a new notion of contour depth with three defining characteristics. First, ID is a generalization of functional Half-Region Depth, which offers several theoretical guarantees. Second, ID relies on a simple principle: the inside/outside relationships between contours. This facilitates implementing ID and understanding its results. Third, the computational complexity of ID scales quadratically in the number of members of the ensemble, improving CBD's cubic complexity. This also in practice speeds up the computation enabling the use of ID for exploring large contour ensembles or in contexts requiring multiple depth evaluations like clustering. In a series of experiments on synthetic data and case studies with meteorological and segmentation data, we evaluate ID's performance and demonstrate its capabilities for the visual analysis of contour ensembles.