IEEE VIS 2024 Content: Critical Point Extraction from Multivariate Functional Approximation

Critical Point Extraction from Multivariate Functional Approximation

Guanqun Ma - University of Utah, Salt Lake City, United States

David Lenz - Argonne National Laboratory, Lemont, United States

Tom Peterka - Argonne National Laboratory, Lemont, United States

Hanqi Guo - The Ohio State University, Columbus, United States

Bei Wang - University of Utah, Salt Lake City, United States

Screen-reader Accessible PDF
Download preprint PDF

Room: Bayshore III

2024-10-14T16:00:00ZGMT-0600Change your timezone on the schedule page
2024-10-14T16:00:00Z
Exemplar figure, described by caption below
Critical points identified by CPE-MFA and TTK-MFA. CPE-MFA: our method in a continuous domain. TTK-MFA: a discrete approach implemented in the topology tool kit. Yellow means the perfect alignment between CPE-MFA and TTK-MFA. Purple represents the critical points from TTK-MFA. Pink represents the critical points from CPE-MFA.
Fast forward
Abstract

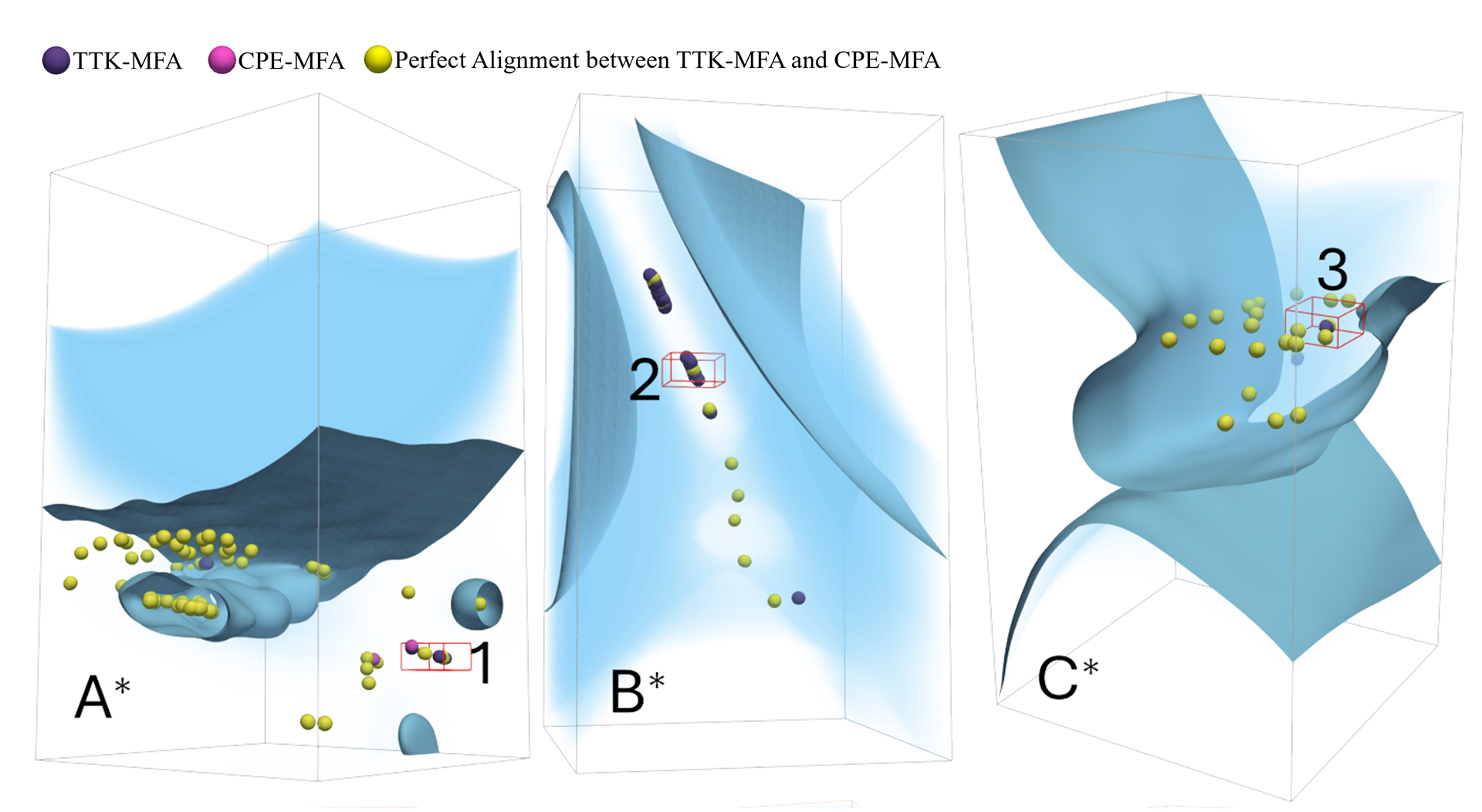
Advances in high-performance computing require new ways to represent large-scale scientific data to support data storage, data transfers, and data analysis within scientific workflows. Multivariate functional approximation (MFA) has recently emerged as a new continuous meshless representation that approximates raw discrete data with a set of piecewise smooth functions. An MFA model of data thus offers a compact representation and supports high-order evaluation of values and derivatives anywhere in the domain. In this paper, we present CPE-MFA, the first critical point extraction framework designed for MFA models of large-scale, high-dimensional data. CPE-MFA extracts critical points directly from an MFA model without the need for discretization or resampling. This is the first step toward enabling continuous implicit models such as MFA to support topological data analysis at scale.